What is vibration?
In very simple terms vibration is an oscillatory movement of small amplitude. All bodies have a vibration signal in which are reflected each of their characteristics. According to this, every machine features its own vibration signal containing information coming for each of its components. In other words, a vibration signal captured from a machine is composed of the sum of the vibration of each of its components.
Simple vibration
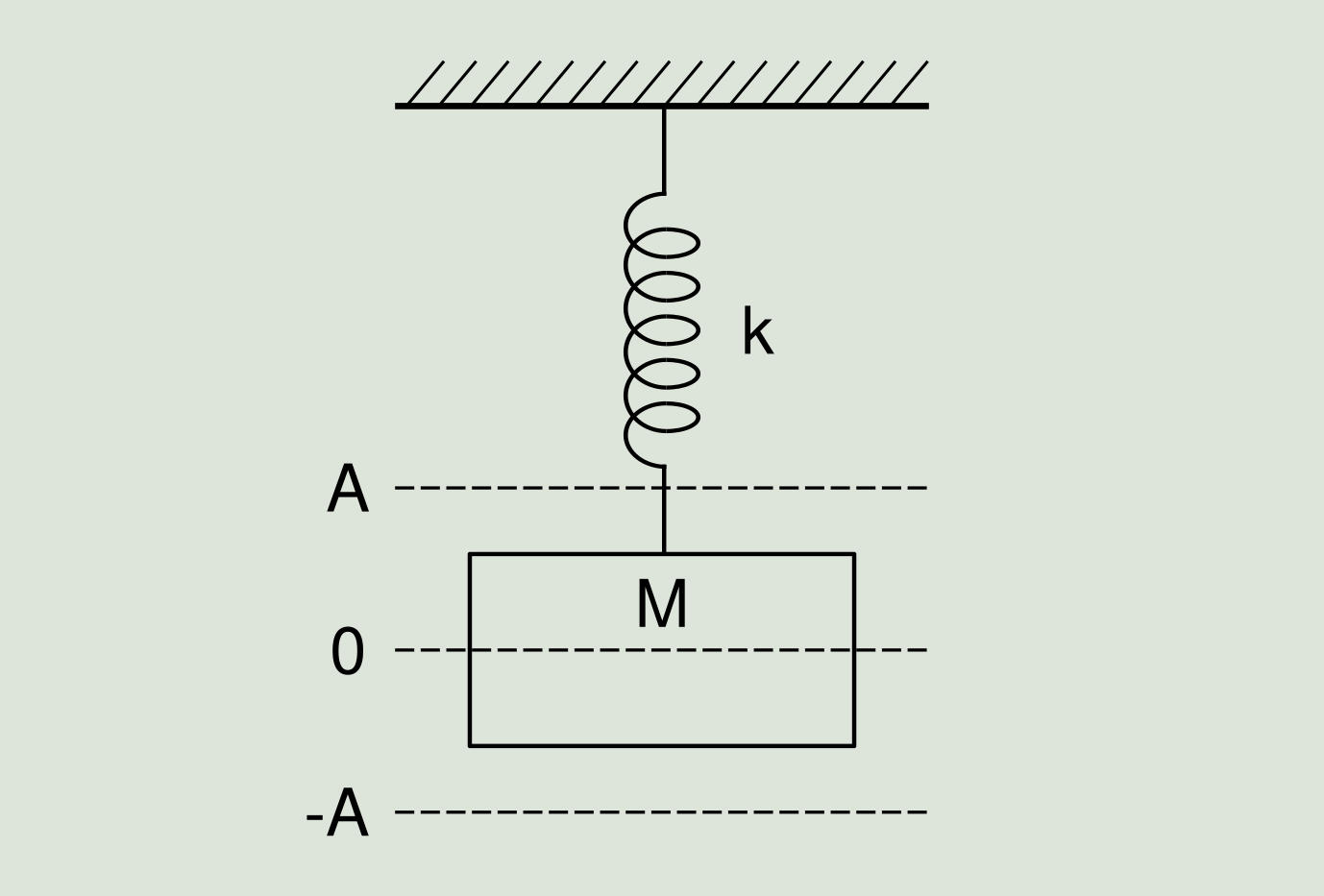
The fundamental component of vibration signals in the time domain are sinusoidal waves. These are the simplest and are the representation of pure oscillations. A pure oscillation can be physically represented by the following experiment: imagine a mass suspended from a spring like the one of Figure 2.1. If this mass is released from a distance A, under ideal conditions, a simple harmonic motion will take place that will have an amplitude A.
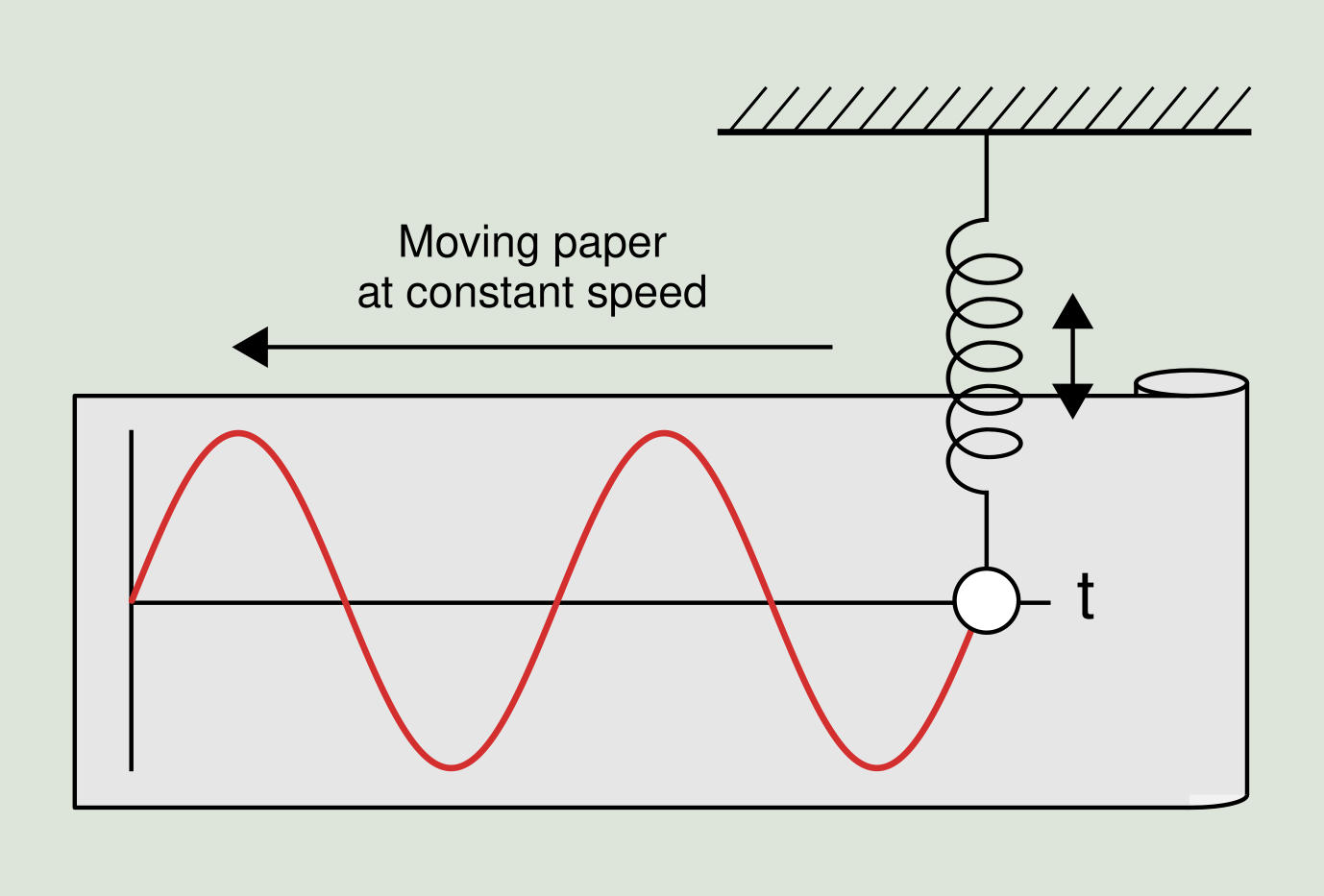
Now we add a pencil and a sheet of paper to the vibrating mass so that it can mark its position. Moving the paper with a constant velocity to the left side will draw a wave as shown in Figure 2.2. The three parameters that define this type of vibration (frequency, amplitude and phase) are described below.
Amplitude
The amplitude from the point of view of vibration is how much a mass can move from a neutral position (marked as 0 in Figure 2.1). It is the intensity of the vibration, and is indicative of the vibration severity.
There are several ways of measuring wave amplitude as shown in Figure 2.3. We can say that the motion features a peak amplitude (pk) of A mm, since we know that since the curve is symmetric there is also an amplitude -A mm in the opposite direction. We can also say that the curve has a peak-to-peak displacement value (pk-pk) of 2A, corresponding to A mm upwards and A mm downwards.
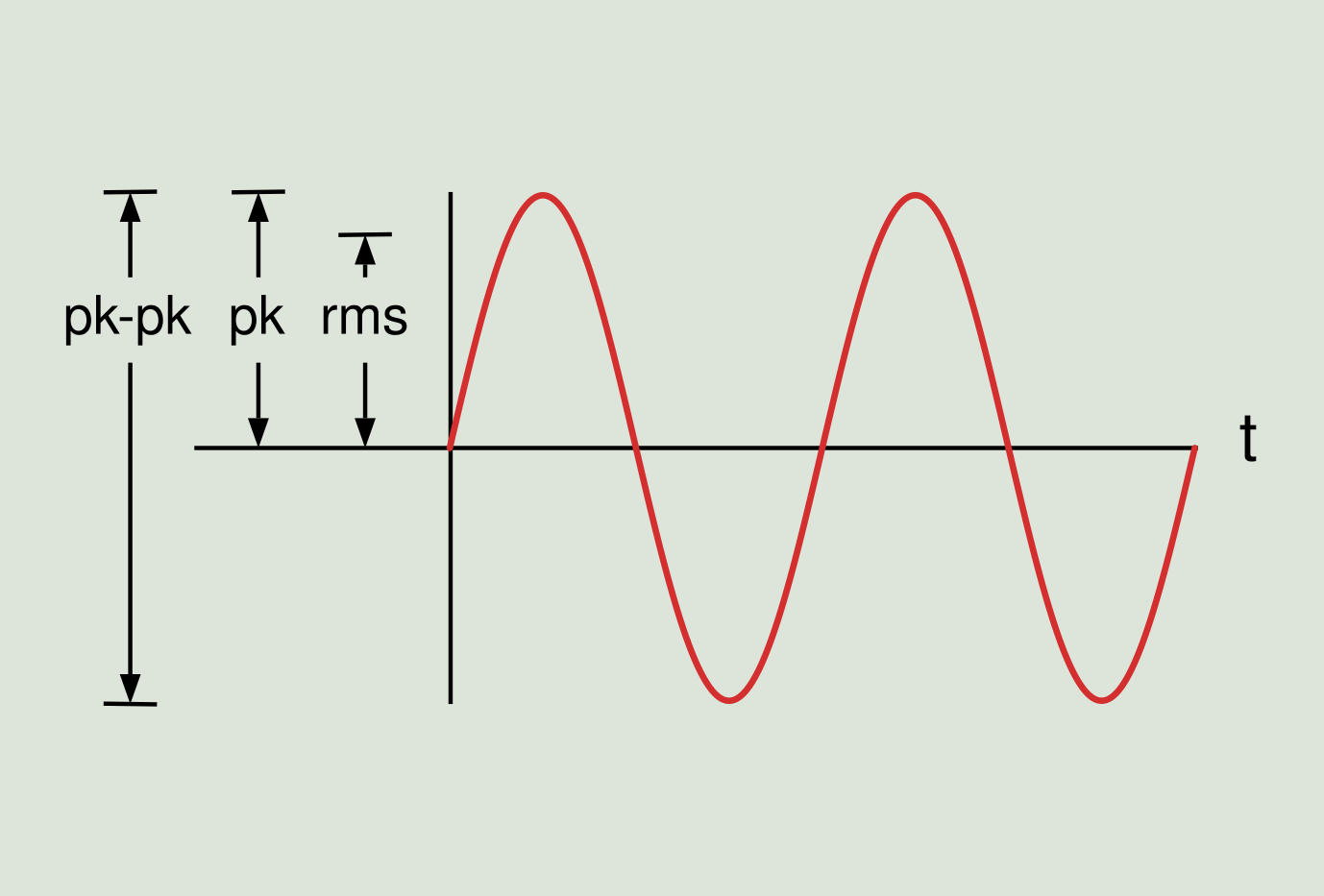
The third way of describing the amplitude is called the RMS (root-mean-square) value and is a bit more complex. It is the square root of the average of the squares of the wave values. In the case of a sine wave the RMS value is equal to 0.707 of the peak value, but this is only valid in the case of a sine wave. The RMS value is used to measure the energy of the waveform.
Frequency
The time it takes for the mass to go back to point A is always constant. This time is called the oscillation period (usually measured in seconds or milliseconds) and means that the spring completed a cycle. The inverse of the period is the frequency (in other words F = 1 / P) which is generally given in Hz (cycles per second) or CPM (cycles per minute).
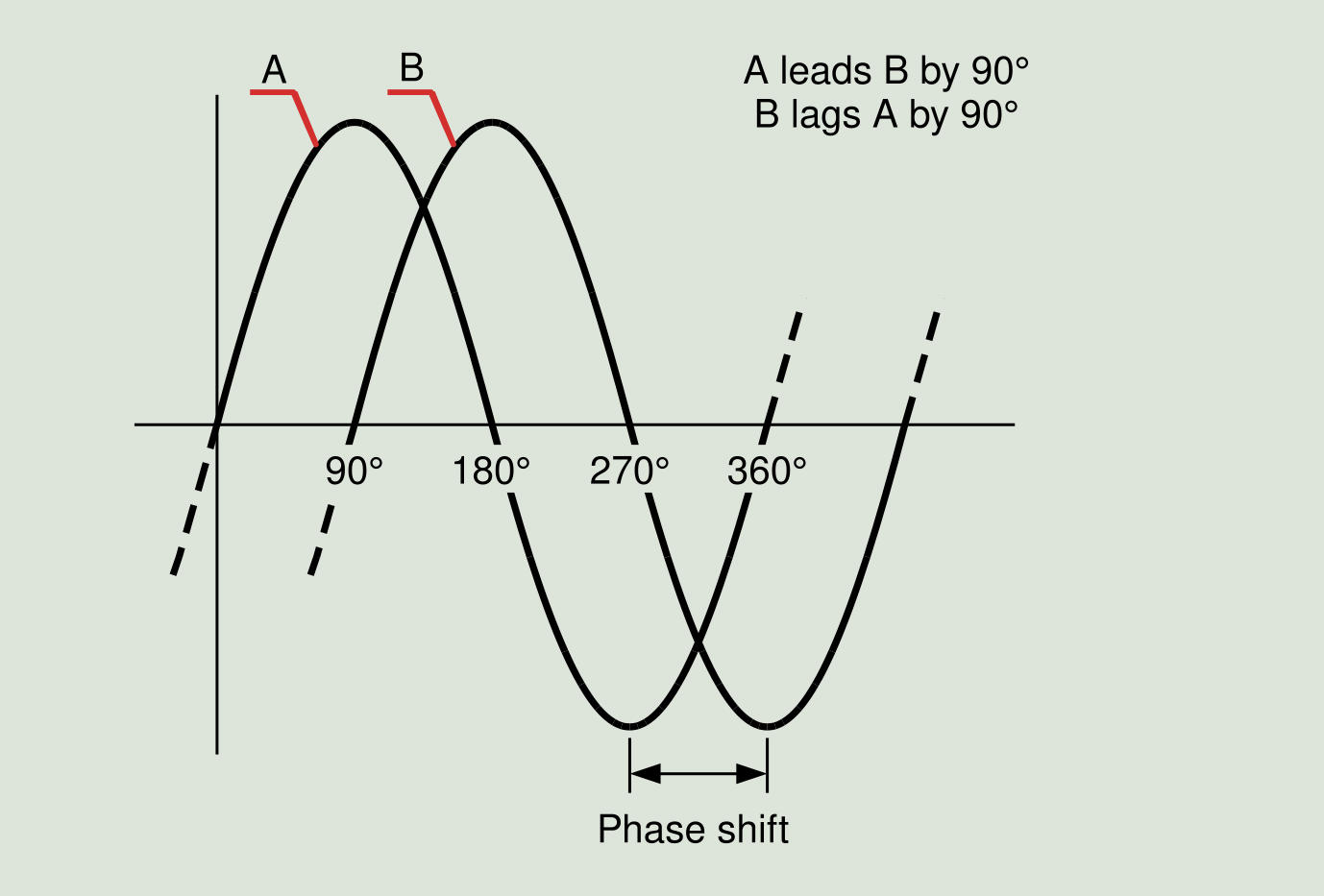
Phase
It is a measure of the time difference between two sine waves. Although the phase is a time difference, it is always measured in terms of angle, degrees, or radians. That is a normalization of time that uses a full wave cycle as a reference without considering its true period of time. The difference in phase between two waveforms is called phase offset or phase shift. A 360-degree phase shift is a one-cycle delay or an entire wave period, which is really phase shift. A phase shift of 90 degrees is a shift of ¼ of the period of the wave, etc. Phase shift can be considered positive or negative; that means that one waveform may be delayed with respect to another or may be ahead of another. These phenomena are called phase lag and phase lead respectively. In the example of Figure 2.4, curve A is shifted 90 degrees with respect to curve B. That is a time delay of ¼ of the wave period. You could also say that curve A has a phase lead of 90 degrees.