Frecuencias propias de un engranaje
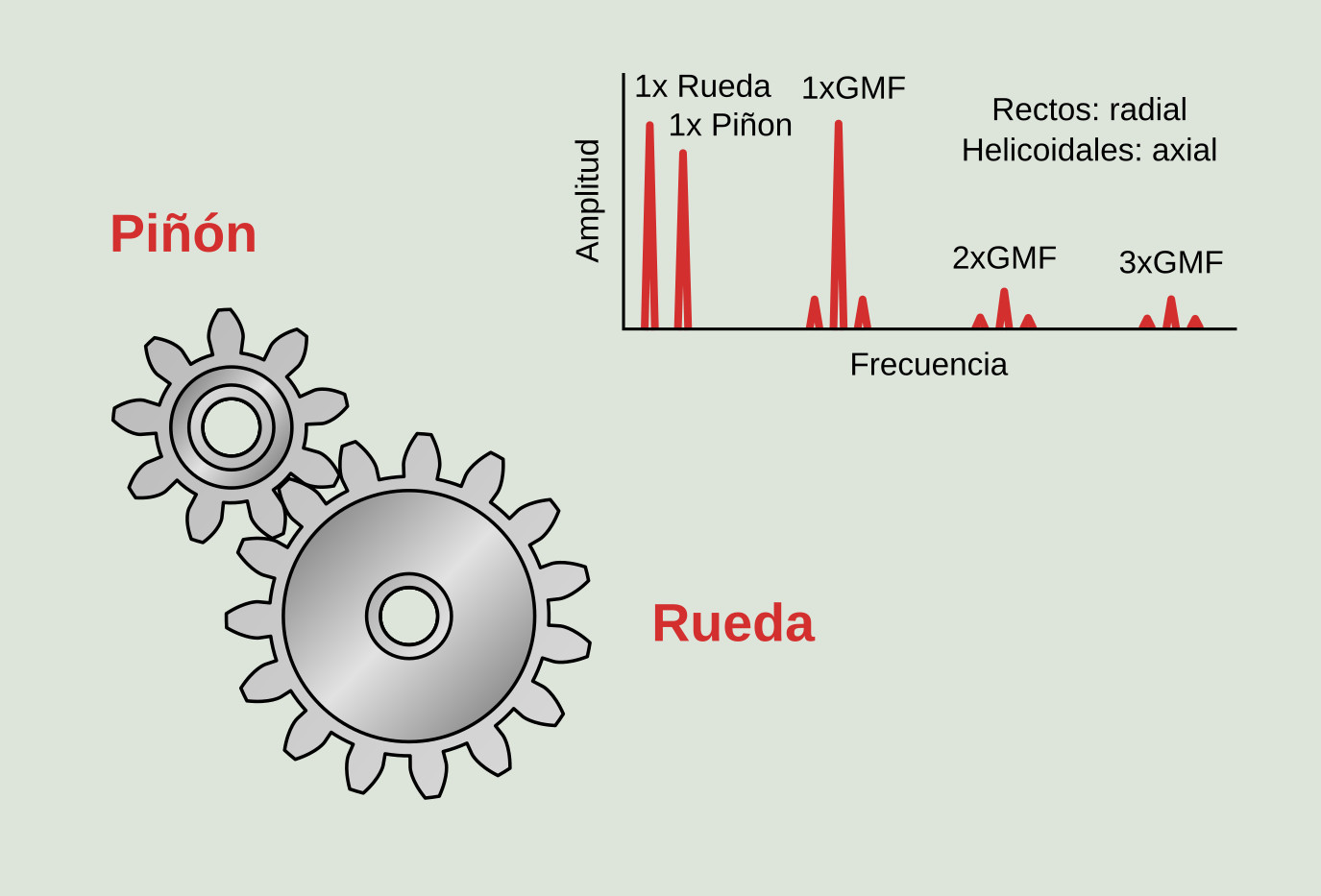
La localización de todas las frecuencias espectrales de un engrane pasa por conocer unos datos mínimos de la caja de engranajes. Estos datos son la velocidad de giro del eje de entrada o el de salida y el número de dientes de las diferentes ruedas dentadas. Las frecuencias asociadas directamente con un engranaje son las siguientes:
- Frecuencia de engrane (GMF): es propia de cada engranaje y aparece en el espectro de frecuencia independientemente del estado del engranaje. Su amplitud depende significativamente de la carga en el momento de la lectura. Se calcula mediante la siguiente fórmula donde, Z es el número de dientes y RPM la velocidad de giro de la rueda dentada.
`sf "GMF" = sf "Z"_sf "P" xx sf "RPM"_sf "P" = sf "Z"_sf "C" xx sf "RPM"_sf "C"`
- Bandas laterales de la frecuencia de engrane: son frecuencias equidistantes a la frecuencia de engrane. Estas bandas laterales se corresponden con la frecuencia de giro del piñón y de la corona. Son muy importantes en el diagnóstico del engrane, ya que indican si la corona o el piñón se encuentran en mal estado.
- Frecuencia de repetición de diente (FRD): para su cálculo hay que calcular previamente el número de fases de ensamblaje (NE) tal y como se explica en el apartado siguiente. Indica la frecuencia con la que un diente de la corona vuelve a engranar con el mismo diente del piñón. En caso de que se produzca un daño en un diente de la corona y otro del piñón, el máximo de vibración tendrá lugar cuando ambos fallos respectivos entren en contacto. Esta frecuencia es muy baja por lo que es difícil localizarla en el espectro de frecuencias, detectándose con mayor facilidad en la forma de onda en el tiempo.
`sf "FRD" = (sf "GMF" xx sf "N"_sf "E") / (sf "Z"_sf "P" xx sf "Z"_sf "C")`
- Frecuencia de fase de ensamblaje (FFE): indica que como consecuencia del desgaste, el espacio entre dientes y su perfil ha cambiado.
`sf "FFE" = sf "GMF" / sf "N"_sf "E"`
- Frecuencias naturales del engranaje: cuando se desarrolla algún tipo de deterioro en el engrane se puede provocar la excitación de las frecuencias naturales del engranaje.
- Frecuencias fantasma: están relacionadas con un defecto relativamente poco frecuente que se manifiesta como una frecuencia típicamente más alta que la GMF pero no directamente relacionada con la geometría del engranaje. Es debido a errores de fabricación que son debidos a vibración en el tren de fabricación y se puede típicamente relacionar con el número de dientes y la velocidad de la máquina de corte.
Cálculo del número de fases de ensamblaje
Definiremos el concepto de fase de ensamblaje como los diferentes modos de engranar que tienen un par de ruedas dentadas. En la siguiente figura se presenta un par de ruedas dentadas, una con 15 dientes y la otra con 9. Se numeran los dientes de las dos ruedas y se obtiene gráficamente que hay tres formas diferentes de montar el engrane. Esto significa que hay tres posibles pautas de desgaste al engranar la corona y el piñón. Para el par corona-piñón de nuestra figura serían: primera fase de ensamblaje, montando el diente número 1 del piñón entre los dientes 1 y 15 de la corona; segunda fase de ensamblaje, montando el diente número 2 del piñón entre los dientes 1 y 15 de la corona; tercera fase de ensamblaje, montando el diente número 3 del piñón entre los dientes 1 y 15 de la corona.
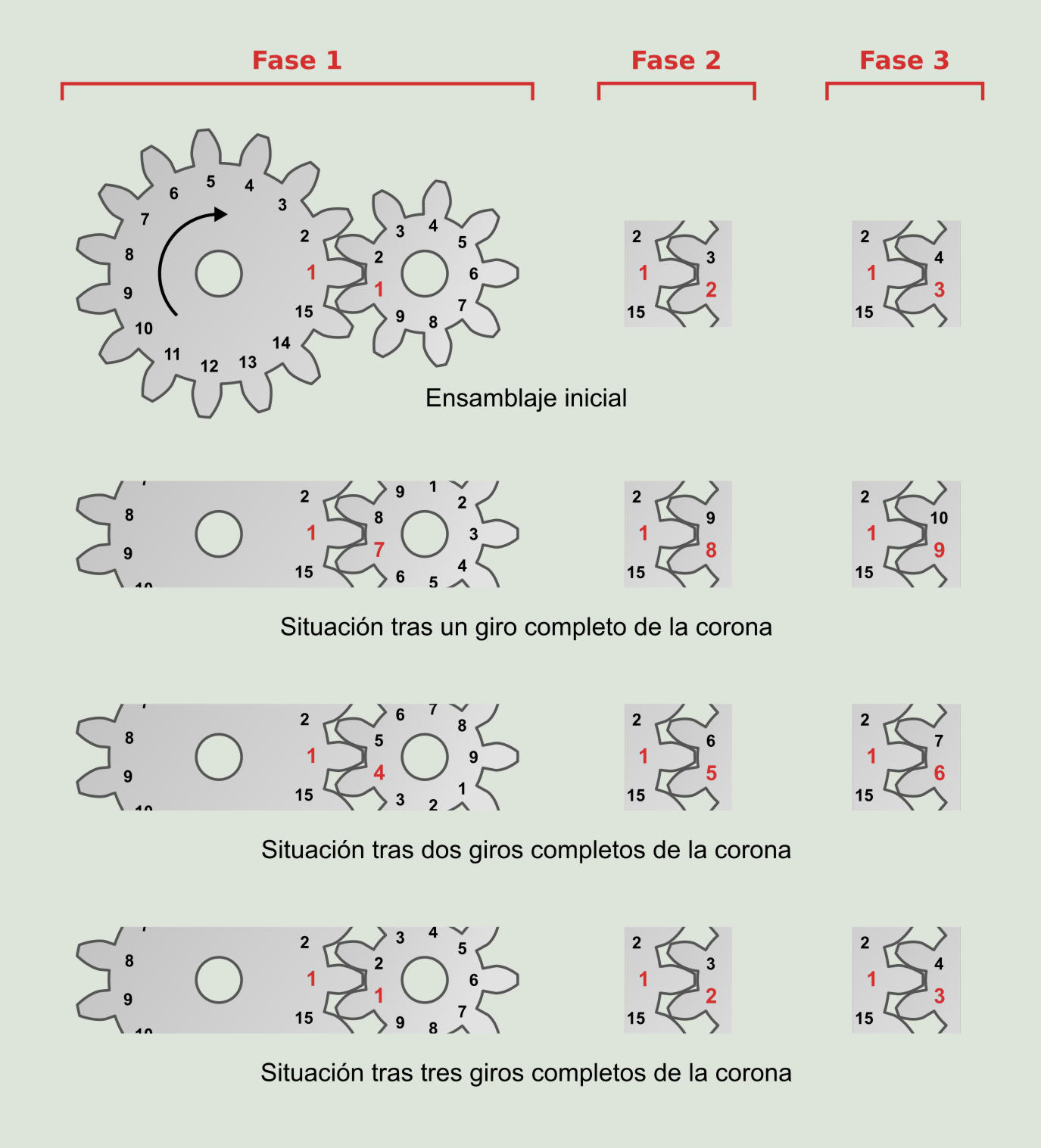
El método matemático para el cálculo de las fases de ensamblaje (NE) se realiza calculando el máximo común divisor del número de dientes de ambas ruedas dentadas. En nuestro caso particular de 15 dientes de la corona, sus factores primos son 5, 3 y 1, ya que 5x3x1 es 15. Los factores primos de los 9 dientes del piñón son 3x3x1. El máximo común divisor es 3x1 que es 3, el mismo número que se había calculado gráficamente.
Cada diente del piñón entrará a engranar con ZC/NE dientes de la corona mientras que cada diente de la corona entrará a engranar con ZP/NE del piñón. Para el caso particular del gráfico de las fases de ensamblaje, se observa que un diente de la corona engrana siempre con los mismos tres dientes del piñón.
Engranajes planetarios
Otro tipo de cajas reductoras o multiplicadoras son aquellas que tienen engranes planetarios. En la siguiente figura se muestran los componentes y la estructura básica de los engranes planetarios.
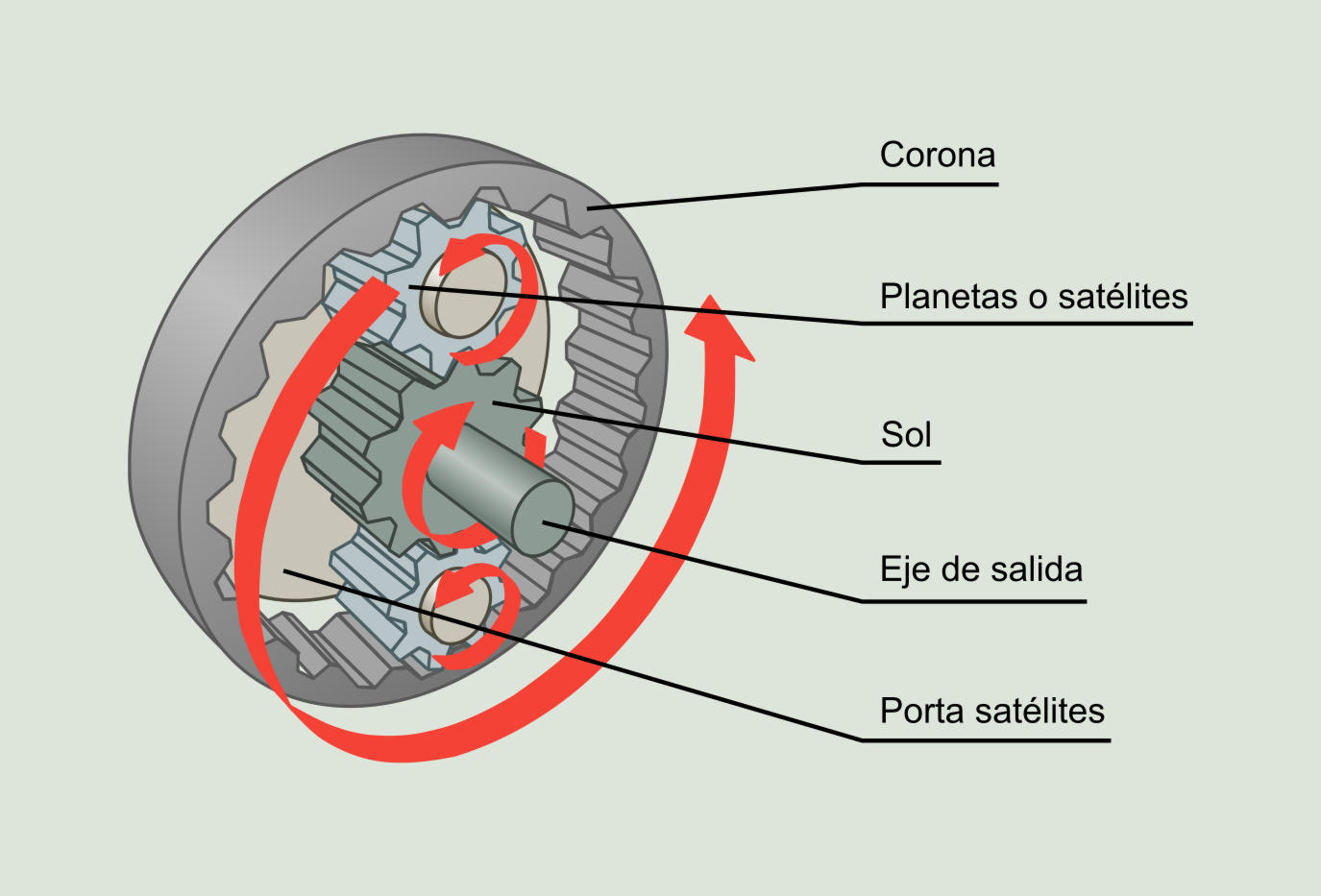
El eje de entrada acaba en un plato llamado porta satélites. El porta satélites está unido con cada uno de los planetas o satélites a través de un eje. Entorno a los planetas hay una rueda dentada de gran tamaño y estacionaria, llamada corona. Los planetas engranan simultáneamente con la corona y con el sol, que es la rueda dentada conectada con el eje de salida.
Su relación de transmisión se calcula de la siguiente forma:
`sf "R"_sf "T" = 1 + sf "Z"_sf "CORONA" / sf "Z"_sf "SOL"`
donde Z denota el número de dientes de un engranaje dado.
La velocidad de giro de cada engranaje planeta se calcula de la siguiente forma:
`sf "RPM"_sf "PLANETA" = sf "RPM"_sf "PORTA SATÉLITES" sf "Z"_sf "CORONA" / sf "Z"_sf "PLANETA"`
La frecuencia de engrane de un sistema de engranajes planetarios es:
`sf "GMF" = sf "Z"_sf "PLANETA" xx sf "RPM"_sf "PLANETA"`
Un defecto en la corona se podrá ver a una frecuencia igual al número de planetas multiplicado por la velocidad de rotación del porta satélites. Un defecto en el sol se mostrará a una frecuencia igual al número de planetas multiplicado por la velocidad de giro del sol menos la velocidad de giro del porta satélites. Por último, un defecto en un planeta aparecerá a una frecuencia igual al doble de la velocidad de giro del planeta.
En esta página:
¿Qué es Power-MI?
Power-MI es una herramienta en la nube que le permite diseñar y gestionar su mantenimiento predictivo con todas las técnicas en una plataforma. Informes fáciles, órdenes de trabajo automáticas e integración a CMMS.
Leer más¿Te gusta esta formación?
cloud_download¡Descarga aquí nuestra versión en formato eBook!