Transformada de Fourier

Hasta ahora sólo hemos visto vibraciones en el dominio del tiempo, que son las señales capturadas directamente de la máquina. Como ya dijimos antes, en estas señales se encuentra plasmada toda la información acerca del comportamiento de cada componente de la máquina. Sin embargo, existe un problema a la hora de realizar un diagnóstico: estas señales están cargadas de mucha información en forma muy compleja, la cual comprende las señales características de cada componente de la máquina, por lo cual prácticamente resulta imposible distinguir a simple vista sus comportamientos característicos.

Existen otras formas para realizar un estudio de vibraciones, entre las cuales se encuentra analizar las señales en el dominio de la frecuencia. Para ello se emplea la gráfica de amplitud frente a frecuencia que es conocida con el nombre de espectro. Esta es la mejor herramienta disponible actualmente para el análisis de maquinaria. Fue precisamente el matemático francés Jean Baptiste Fourier (1768 - 1830) quien encontró la forma de representar una señal compleja en el dominio del tiempo por medio de series de curvas sinusoidales con valores de amplitud y frecuencia específicos.

Entonces lo que hace un analizador de espectros que trabaja con la transformada rápida de Fourier es capturar una señal de una máquina, calcular todas las series de señales sinusoidales que contiene la señal compleja y por último mostrarlas de forma individual en una gráfica de espectro.

En la Figura 2.9 puede verse claramente una representación tridimensional de la señal de vibración compuesta, capturada en un punto de una máquina. Para dicha señal se calculan todas las señales sinusoidales en el dominio del tiempo que la componen y por último se muestra cada una de ellas en el dominio de la frecuencia.

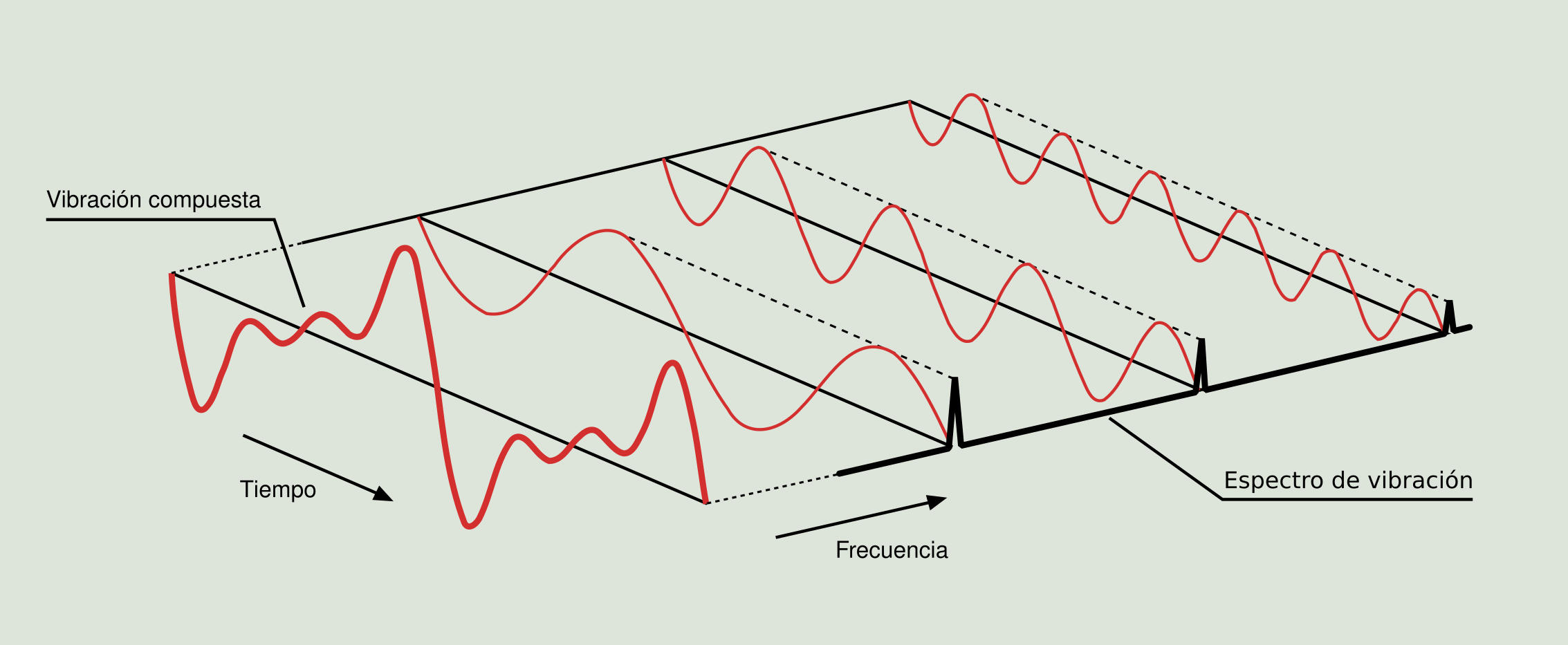
De este modo, empleando la transformada de Fourier, podemos retomar la suma de vibraciones simples de la Figura 2.5 y representar exactamente la misma operación en el dominio de la frecuencia como se muestra en la Figura 2.10, con la particularidad de que en este caso resulta inmediato obtener las frecuencias y amplitudes de las dos componentes originales a partir del espectro resultante.

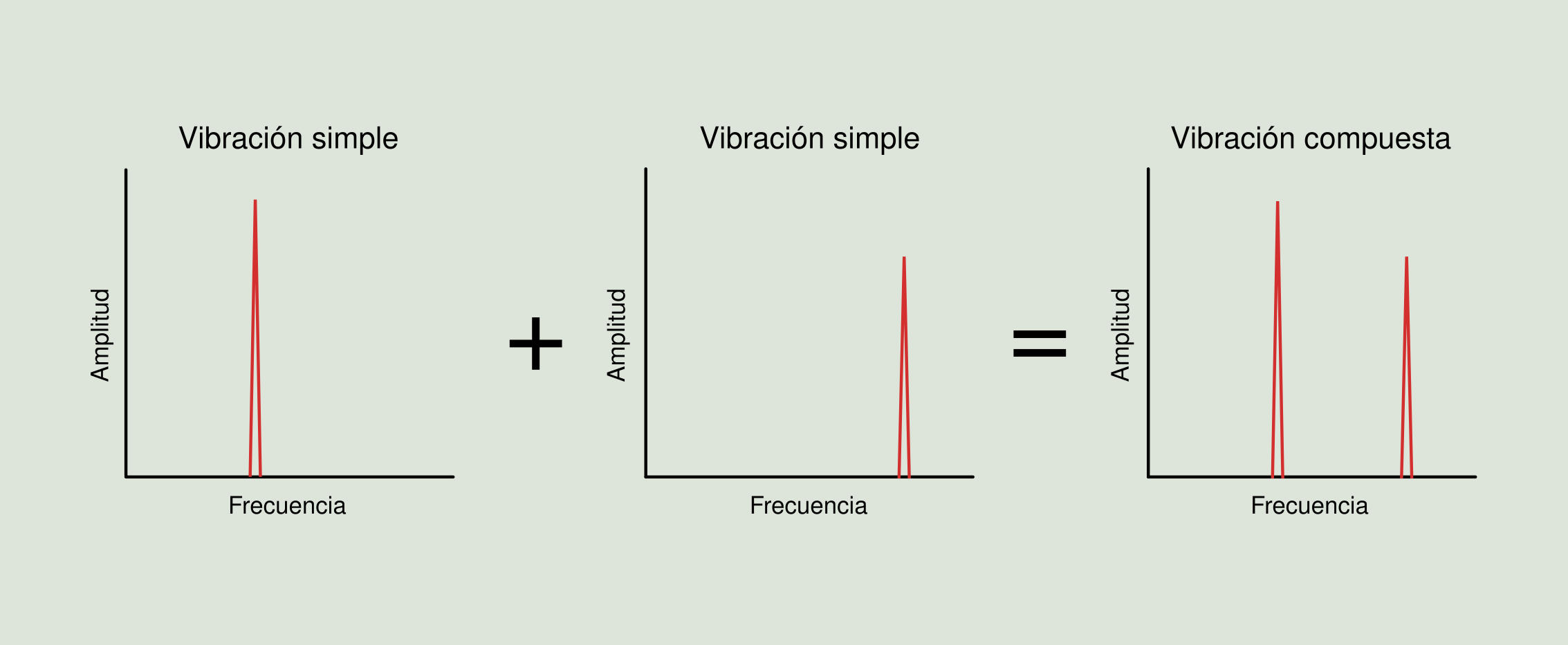
Como ya se ha dicho, la gráfica en el dominio del tiempo se llama la forma de onda, y la gráfica en el dominio de la frecuencia se llama el espectro. El análisis del espectro es equivalente a transformar la información de la señal del dominio de tiempo en el dominio de la frecuencia. Un ejemplo claro de la equivalencia en ambos dominios es un horario, donde podemos decir que sale un tren a las 6:00, 6:20, 6:40, 7:00, 7:20, o podemos decir que sale un tren cada 20 minutos comenzando a las 6:00 (representando este último dato la fase). Lo primero sería la representación en el tiempo y lo segundo la representación en frecuencia. La representación en frecuencia aporta una reducción de datos con respecto a la representación en el tiempo. La información es exactamente la misma en ambos dominios, pero en el dominio de frecuencia esta es representada de una manera más compacta y más práctica.

Desplazamiento, velocidad y aceleración

Hasta ahora, solamente hemos considerado como medida de la amplitud de la vibración de un objeto el desplazamiento. El desplazamiento es sencillamente la distancia al objeto desde una posición de referencia o punto de equilibrio. Aparte de un desplazamiento variable, un objeto que vibra presenta una velocidad variable y una aceleración variable. La velocidad se define como la variación en el desplazamiento y se mide por lo general en in/s (pulgadas por segundo) o mm/s. La aceleración se define como la variación en la velocidad y se mide en g (la aceleración promedio debida a la gravedad en la superficie de la tierra) o mm/s². Como hemos visto, el desplazamiento de un cuerpo que está sometido a un movimiento armónico simple es una onda sinusoidal. También la velocidad y la aceleración del movimiento son ondas sinusoidales.

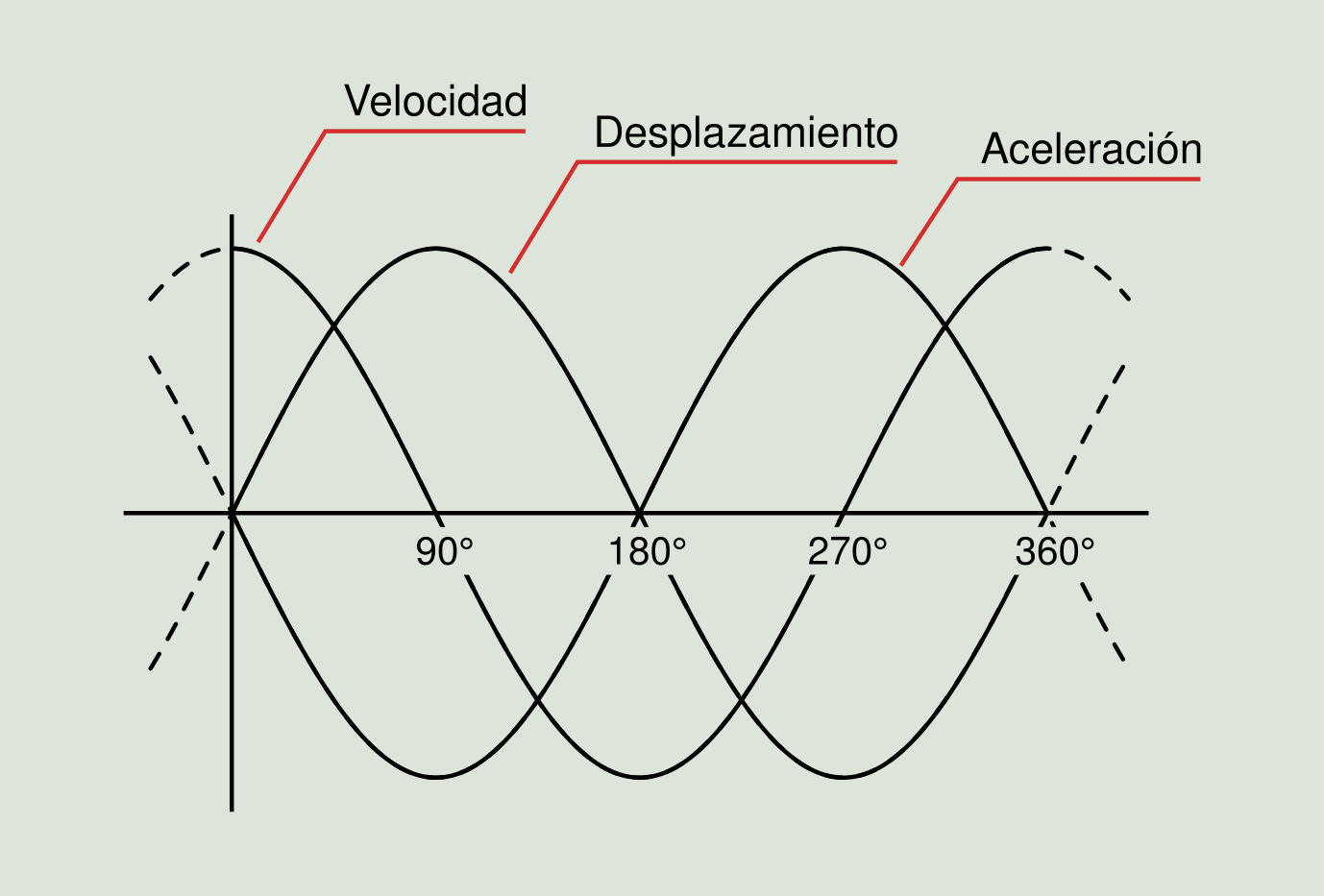
Cuando el desplazamiento alcanza su valor máximo, la velocidad vale cero, porque esa es la posición en la que la dirección del movimiento se invierte. Cuando el desplazamiento vale cero (en el punto de equilibrio), la velocidad estará en su valor máximo. Esto quiere decir que la fase de la onda de velocidad se encontrará desplazada hacia la izquierda 90 grados, comparada con la forma de onda del desplazamiento. En otras palabras, la velocidad está adelantada 90 grados con respecto al desplazamiento. La aceleración es lel nivel de variación en la velocidad. Cuando la velocidad alcanza su valor máximo, la aceleración vale cero ya que la velocidad no cambia en ese momento. Cuando la velocidad vale cero, la aceleración está en su valor máximo en ese momento dado que es cuando más rápido cambia la velocidad. La curva sinusoidal de la aceleración en función del tiempo se puede ver de esta manera como desplazada en fase hacia la izquierda respecto a la curva de velocidad y por eso la aceleración tiene un avance de 90 grados respecto a la velocidad y de 180 grados respecto al desplazamiento.

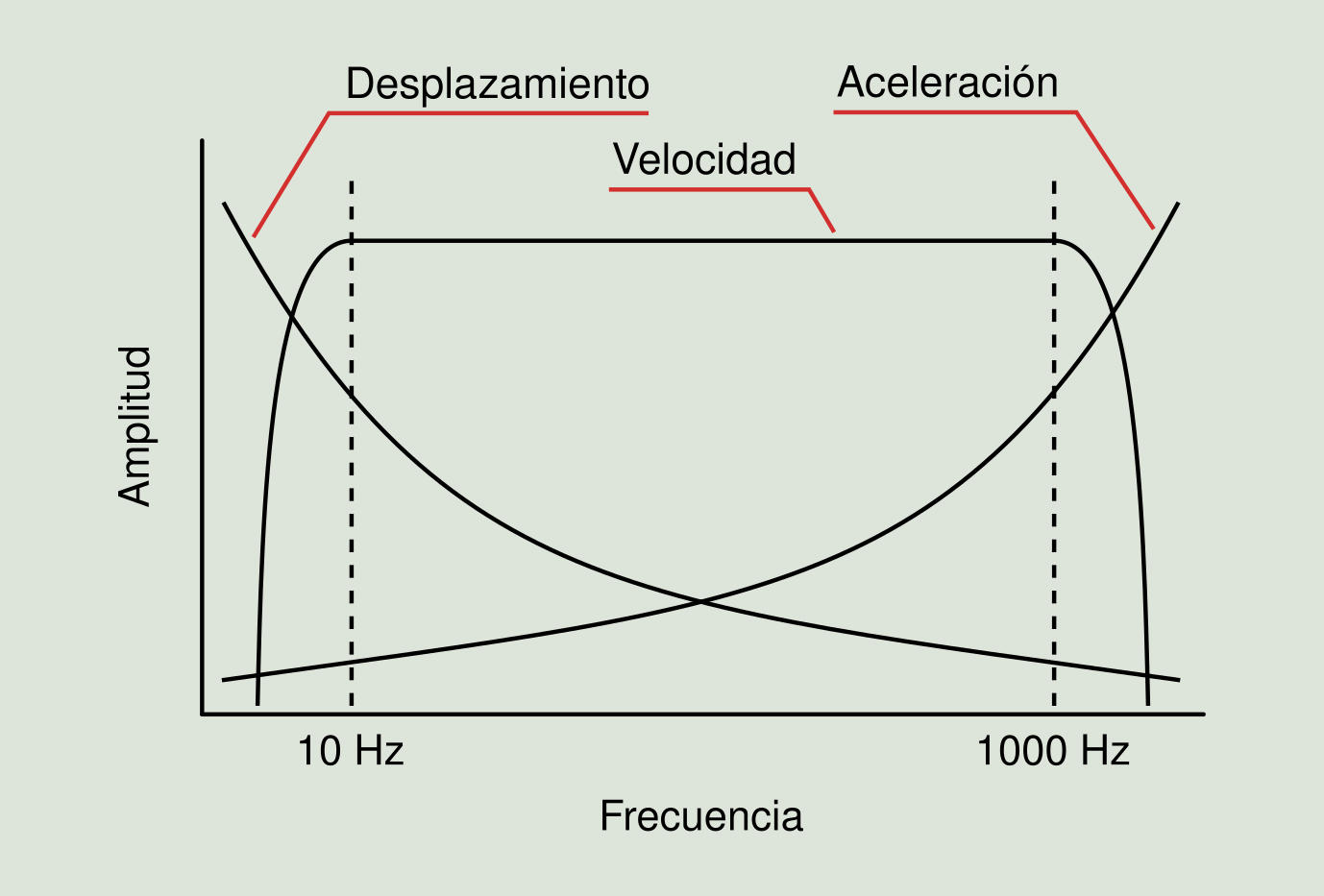
Las unidades de amplitud de vibración empleadas para expresar cada medida tienen gran influencia en la claridad con la cual se manifiestan los fenómenos vibratorios. Así, según se puede ver en la Figura 2.12, el desplazamiento muestra sus mayores amplitudes en bajas frecuencias (típicamente por debajo de 10 Hz), la velocidad lo hace en un rango intermedio de frecuencias (entre 10 y 1.000 Hz), y la aceleración se manifiesta mejor a altas frecuencias (por encima de 1.000 Hz).

Para ilustrar estas relaciones, consideremos lo fácil que resulta mover la mano una distancia de un palmo a un ciclo por segundo o 1 Hz. Probablemente sería posible lograr un desplazamiento similar de la mano a 5 o a 6 Hz. Pero consideremos la velocidad con que se debería mover la mano para lograr el mismo desplazamiento de un palmo a 100 Hz o 1.000 Hz. Esta es la razón por la que nunca se ven niveles de frecuencia altos combinados con valores de desplazamiento altos. Las fuerzas enormes que serían necesarias sencillamente no se dan en la práctica.

En la Figura 2.13 se presenta un gráfico con un ejemplo del comportamiento de las distintas unidades de amplitud en todo el rango de frecuencias. Los tres espectros proporcionan la misma información, pero su énfasis ha cambiado. La curva de desplazamiento es más difícil de leer en las frecuencias más altas. La curva de velocidad es la más uniforme en todo el rango de frecuencias.

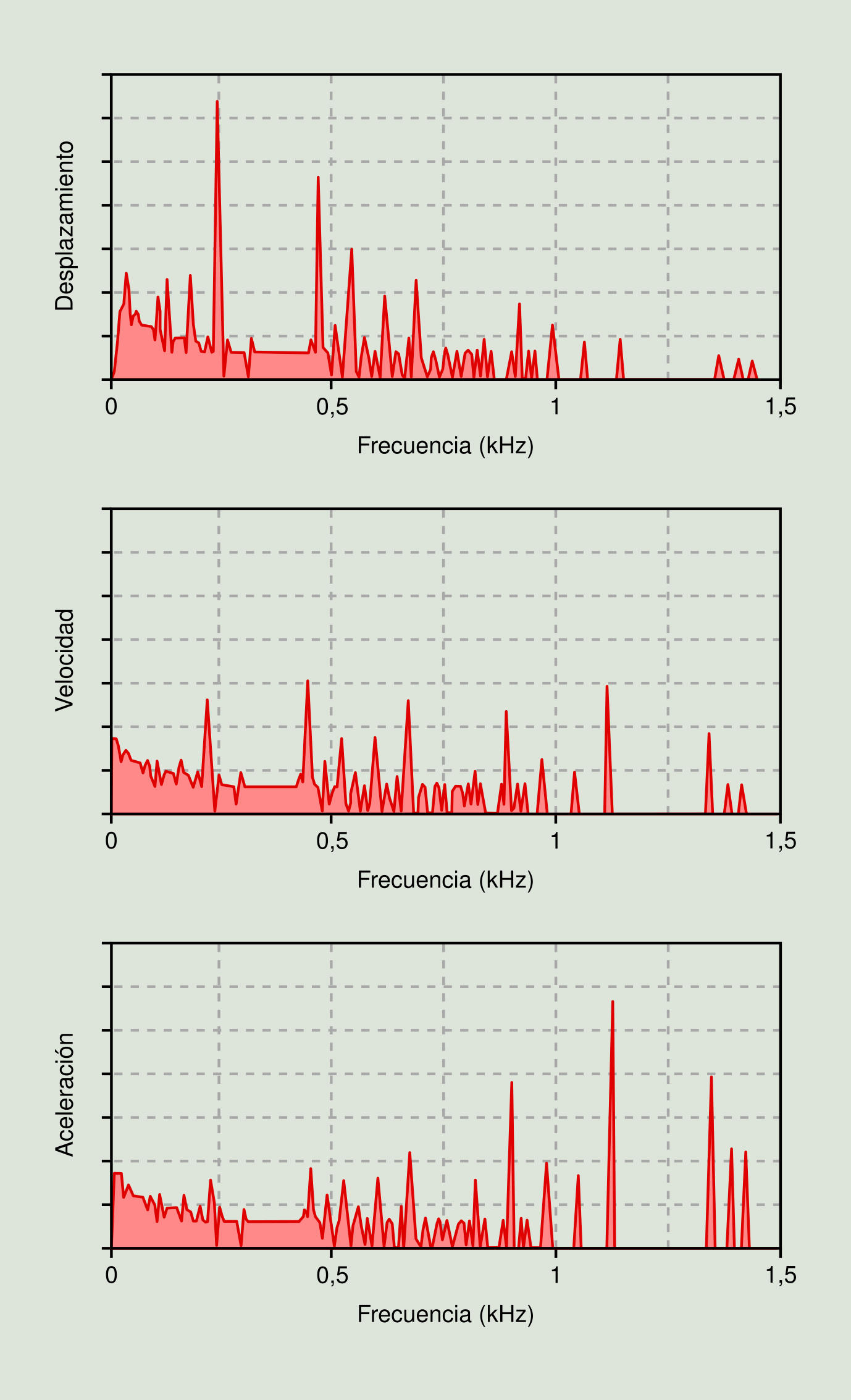
Este es el comportamiento típico para la mayoría de la maquinaria rotativa pero, sin embargo, en algunos casos las curvas de desplazamiento y aceleración serán las más uniformes. Es una buena idea seleccionar las unidades de tal manera que se obtenga la curva más plana. Eso proporciona la mayor cantidad de información visual al observador. El parámetro de vibración que se utiliza más comúnmente en trabajos de diagnóstico de maquinaria es la velocidad.

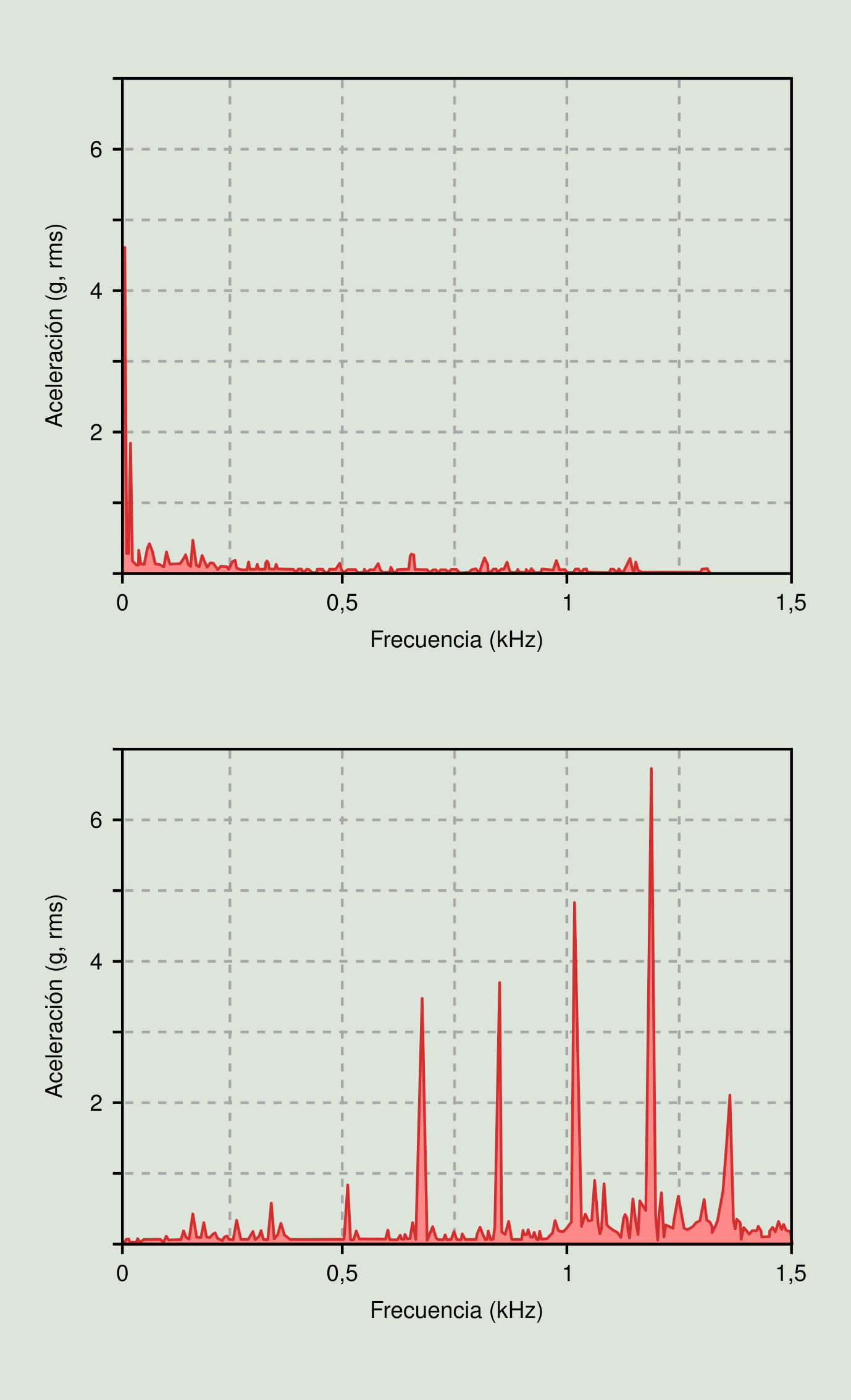
Por último, ilustraremos lo dicho con el caso práctico de la siguiente figura donde se muestra un mismo espectro en unidades de desplazamiento y aceleración. Ambas gráficas corresponden a un deterioro de un rodamiento. En el espectro en desplazamiento no se observa el problema, mientras que en el espectro en aceleración se observa claramente.

Análisis espectral

Cuando se mide la vibración de una máquina, se genera una información muy valiosa que es necesario analizar. El éxito de dicho análisis depende de la correcta interpretación que se le de a los espectros capturados con respecto a las condiciones de operación en que se encuentra la máquina. Los pasos típicos en el análisis de vibración son:

• Identificación de los picos de vibración en el espectro: lo primero es identificar el pico de primer orden (1X), correspondiente a la velocidad de rotación del eje. En máquinas con múltiples ejes, cada eje tendrá su frecuencia de rotación característica 1X. En muchas ocasiones, los picos 1X del eje van acompañados de una serie de armónicos o múltiplos enteros de 1X. Existen armónicos de especial interés, por ejemplo, si se trata de una bomba de seis álabes, normalmente, habrá un pico fuerte espectral en 6X.

• Diagnóstico de la máquina: determinación de la gravedad de problemas de máquina basándose en las amplitudes y la relación entre los picos de vibración.

• Recomendaciones apropiadas para las reparaciones, basadas en la gravedad de los problemas de máquinas.

Consideremos a modo de ejemplo el sistema de la Figura 2.15.

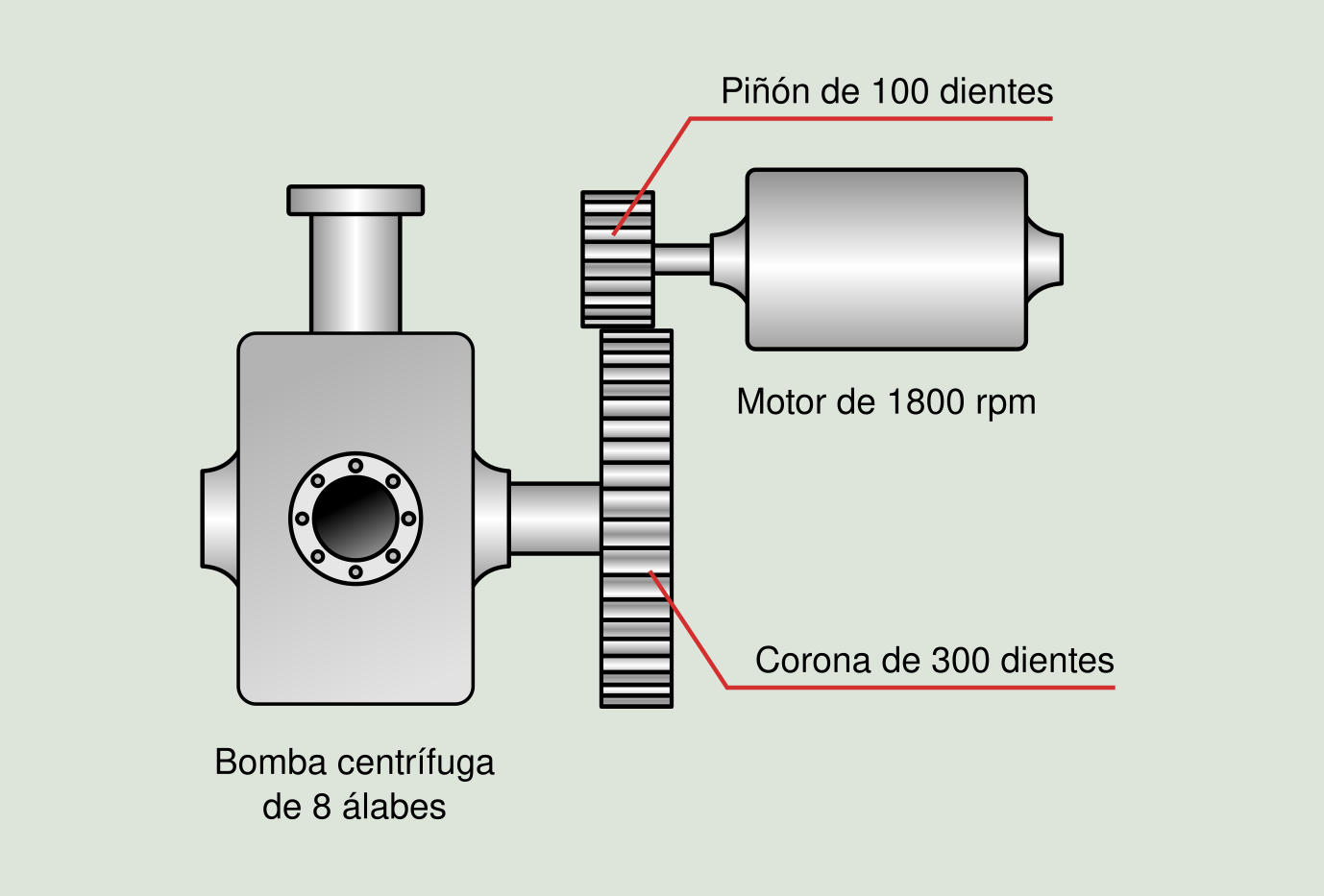
A partir de los datos disponibles podemos calcular las principales frecuencias interés:

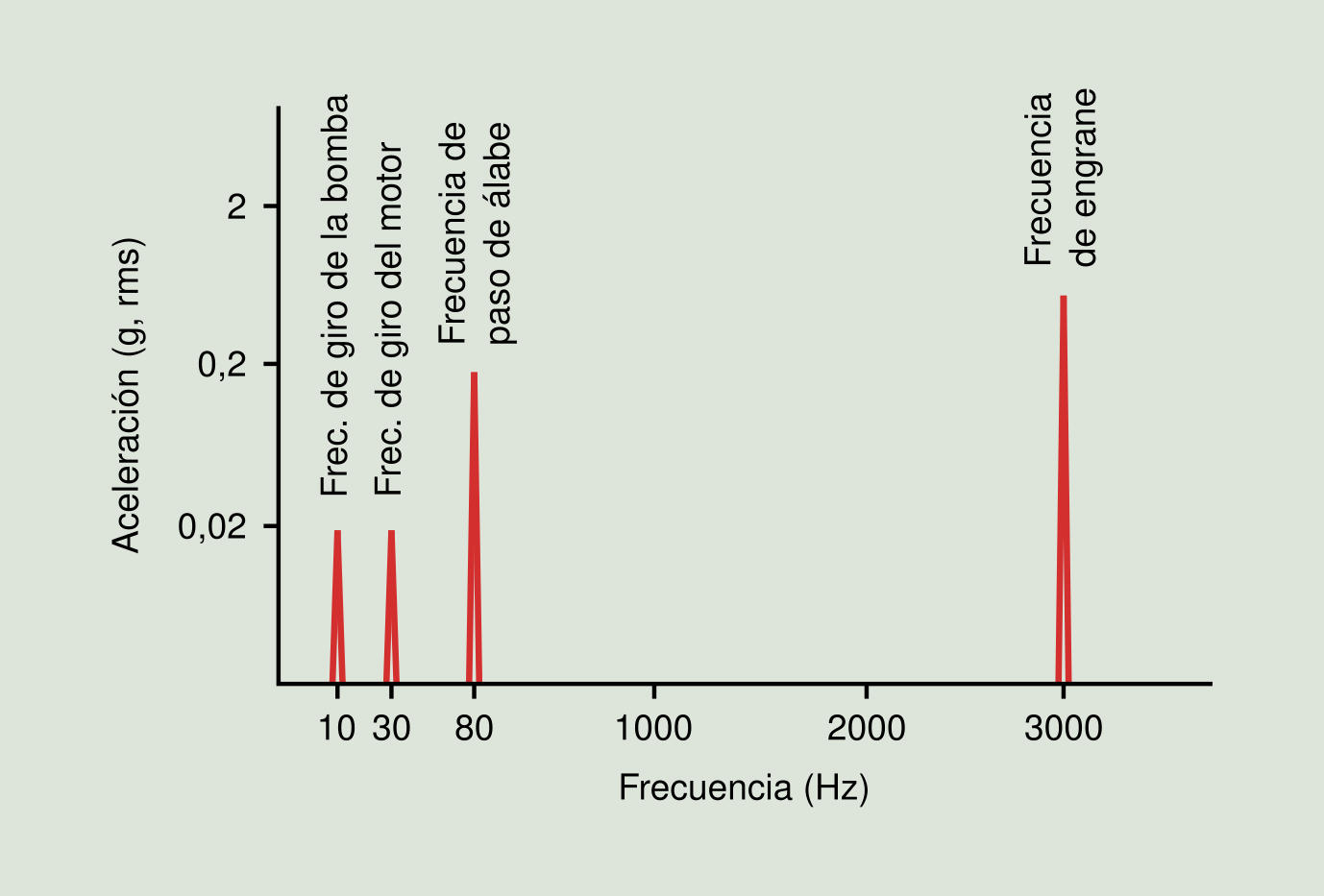
En esta máquina tenemos dos ejes (motor y bomba). En el caso del motor, el valor 1X es 30 Hz, además probablemente encontremos un pico de frecuencia en el espectro en el armónico 100X, que se corresponde con la frecuencia de engrane entre piñon y corona. Para la bomba, el valor 1X es 10 Hz, y su principal armónico de interés es 8X, que se corresponde con la frecuencia de paso de álabe. Obviamente, pueden aparecer otras frecuencias, como por ejemplo, bandas laterales en la frecuencia de engrane, frecuencias de cojinetes, y armónicos de las frecuencias calculadas.

En el espectro de vibración de la Figura 2.16 aparece representada la firma de vibración de nuestro sistema mecánico de ejemplo.

Una vez que hemos identificado las frecuencias de interés, la siguiente cuestión es si el valor de su amplitud es aceptable o inaceptable. Un valor de vibración aceptable es aquel que no causa una reducción en la vida de la máquina ni causa daños en los equipos cercanos. Algunas máquinas están diseñadas para tolerar niveles de vibración extremadamente altos (por ejemplo, molinos) y otros equipos son muy sensibles incluso al más leve nivel de vibración (por ejemplo, sistemas ópticos). Existen cuatro formas de determinar cual es el nivel de vibración adecuado para una máquina dada. La mejor forma es mantener un registro de datos a lo largo del tiempo de los puntos críticos de la máquina, a partir de estos datos se establecerán criterios de referencia de los niveles aceptables. Si existen varias máquinas idénticas en la planta se puede utilizar un segundo método. Si tres máquinas muestran un espectro similar y la cuarta máquina muestra niveles mucho más altos trabajando en las mismas condiciones, es fácil suponer que máquina está teniendo problemas. Otro método es recopilar datos de vibración y enviarlos al fabricante para que los evalúe. Hay que tener en cuenta que la vibración varía en función de las condiciones de trabajo y del montaje de la máquina. El cuarto método es elegir un estándar en base a la experiencia de otros y si es necesario adaptarlo en base a nuestra experiencia.